M5P:預測非線性連續資料的樹狀迴歸演算法 / M5P: Trees with Linear Models in Weka
M5P樹狀迴歸演算法是Weka內建的一種迴歸演算法。它可根據資料的分佈建立多種迴歸模型,依據輸入資料的不同來決定適用的迴歸模型。比起傳統的線性迴歸,M5P能夠準確預測非線性的資料,而且規則與迴歸模型容易解讀。相較於類神經網路和支持向量機等黑箱演算法,白箱演算法的M5P更容易用於研究結果的解釋上。
問題背景 / Background
(圖片來源:自由時報)
用數值來預測數值的問題叫做「迴歸」(regression),而「迴歸」的經典演算法是線性迴歸(Linear Regression)。線性迴歸能夠有效處理具有明確線性規律的資料,像是緯度的高低跟氣溫之間的關係,這可以讓我們容易用多元迴歸來解釋資料的規律。但是若資料呈現非線性的分佈,那線性迴歸的效果就很差。舉例來說,月份跟氣溫的關係就不是單純的線性關係。較小跟較大的月份接近冬季,氣溫較低;位於中間的月份接近夏季,氣溫較高,這樣的情況就是非線性資料。
處理非線性資料時,常見的做法會採用類神經網路(多層次感知機或深度學習,也就是現在流行的AI)或是支持向量機的迴歸演算法SMOreg。但是這些黑箱演算法所建立的預測模型無法讓人解讀,對於解釋研究結果的幫助有限。
這時候,M5P樹狀迴歸預測演算法就是最佳的解決方案啦。
M5P演算法 / M5P: Induction of model trees for predicting continuous classes
(圖片來源:WAIKATO大學的Research Commons)
M5P是Yong Wang與Ian H. Witten在1996年發表的機器學習演算法。引用書目如下:
Wang, Y., & Witten, I. H. (1996). Induction of model trees for predicting continuous classes (Working Paper). Retrieved from http://researchcommons.waikato.ac.nz/handle/10289/1183
以下是該論文的摘要:
在實務上,許多機器學習研究問題要預測的「預測目標」(class)大多都是連續數值,然而只有少數的機器學習方法能夠處理連續數值的預測。這篇論文介紹了一種M5演算法的「原理重建」("rational reconstruction" of M5)。M5是Quilan (1992)發展的一種歸納樹狀迴歸模型的預測方法。為了處理實務上的資料,我們必須要求處理大量屬性(attributes,也就是輸入資料)跟缺失值(missing values),而這個技術來自於Breiman等人(1984)。在分析了既有資料之後,研究結果發現效果高於M5演算法。
演算法的細節請看論文本身。以下我們就不談理論,直接來實作吧!
資料 / Data
這份資料是來自於臺灣交通部中央氣象局的氣候統計1981年至2010年的各地月平均。原始資料羅列了淡水、鞍部、臺北到臺東、梧棲等25個地點的1月到12月的平均氣溫,我僅取月份與氣溫組成了上面的資料集month_temperature,請下載CSV檔案:month_temperature - data.csv。
在month_temperature這份資料集中,我們要用月份month來預測氣溫temperature。我將月份與氣溫畫成了上面的散佈圖。每個月的氣溫有很多個點,這是因為地點不同所導致。但這次的問題我們不考慮地點,僅看月份本身。從散佈圖中可以看到不同月份的氣溫分佈不太一樣。大致上來說,1月到3月、12月等的氣溫較低,6月到9月的氣溫較高,由此就可以看出冬季與夏季的差別。
這次是因為輸入資料(屬性)只有一個,而且是我們熟悉的月份,所以我們容易看出資料的規律。若是在實際應用時,輸入的資料往往高達二三十項。要如何找出資料的規律,並建構出能夠準確預測的模型,就要藉助M5P演算法的技術了。
環境配置:Weka / Environment: Weka
本實作使用的是Weka 3.8.1。M5P是Weka內建演算法,不需要額外安裝套件。Weka的下載與安裝請看下面的文章:
Step 1. 開啟CSV檔案 / Open CSV file
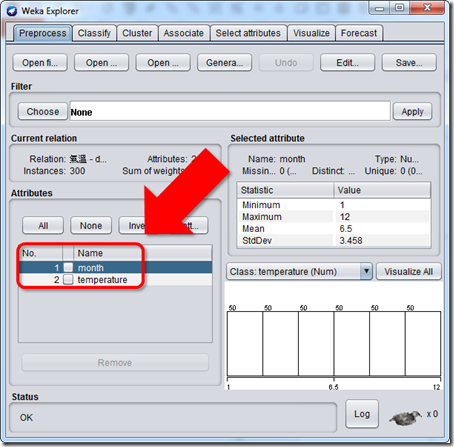
開啟Weka,進入Explorer,然後按左上角的「Open file」開啟檔案。
開啟檔案的時候,Files of Type要記得選擇「CSV data files (*.csv)」,這樣才能看到剛剛下載的CSV檔案:month_temperature - data.csv。
看到Attributes正確出現了month跟temperature兩個屬性,那就表示正確載入了。
Step 2. 使用M5P建立預測模型 / Build prediction model with M5P
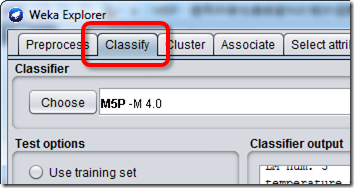
接下來切換到Classify面板來進行預測吧。
分類器Classifier請選擇trees裡面的M5P。
再來什麼都不用調整,就直接按下「Start」,右邊就出現建模結果了。這一步還蠻簡單的。
Step 3. 解讀模型結果 / Explain the model
接下來我們要針對右邊的建模結果進行解讀。
平均絕對誤 / Mean absolute error
在最後的「Summary」摘要裡面可以看到以下資訊:
Mean absolute error 3.2438Mean absolute error 平均絕對誤,又稱平均偏差,這是評估預測模型最簡單的一個指標。這表示所有預測值跟實際值之間偏差的平均。以本例來說,若以M5P建立的預測模型,用月份來預測氣溫,則平均每次都會誤差個3.2438度。
模型樹 / Model tree
往上看到「Classifier model (full traning set)」,這是M5P建構的預測模型。我們先來看模型樹的部分:
month <= 3.5 : LM1 (75/75.485%)
month > 3.5 :
| month <= 10.5 : LM2 (175/83.248%)
| month > 10.5 : LM3 (50/73.756%)在本例中,M5P建構了3個線性迴歸模型,各別是LM1、LM2跟LM3。模型樹用if-else的結構來表示什麼時候適用哪種線性迴歸模型的時機。用文字來敘述的話,上面的模型樹的意思是:
- 如month小於或等於3.5,則適用LM1模型來預測。
- 如果month大於3.5,則繼續看下面的規則。
- 如果month小於或等於10.5,則適用LM2模型。
- 如果month大於10.5,則適用於LM3模型。
因為我們的month月份只有1到12,換句話說:
- 1月到3月:適用LM1
- 4月到10月:適用LM2
- 11月與12月:適用LM3
仔細一看,1月到3月、11月與12月偏向冬季,4月到10月則偏向夏季。M5P在建構預測模型時就很敏銳地發現到了月份與季節的關係呢。
線性模型 / Linear Models
那LM1、LM2跟LM3到底是什麼呢?讓我們繼續往下看。
LM num: 1
temperature =
1.1281 * month
+ 14.8548
LM num: 2
temperature =
0.2922 * month
+ 22.1745
LM num: 3
temperature =
-2.4283 * month
+ 47.4147這裡列出了三個線性模型,LM num: 1就是LM1、LM num: 2則是LM2、那LM num: 3就是指LM3。
適用1月到3月的LM1 / For Jan. to Mar. : LM1
我以LM1為例來說明線性模型的意思:
LM num: 1
temperature = 1.1281 * month + 14.8548這個意思是,月份乘上1.1281,再加上截距14.8548,就是氣溫的預測值。由於月份的係數為正數,表示1月到3月間,月份越大、氣溫越高。
適用11月與12月的LM3 / For Nov. and Dec. : LM3
反觀LM3這個線性模型,我們可以看到不同的結果:
LM num: 3
temperature = -2.4283 * month + 47.4147氣溫的預測值是月份乘上-2.4283,再加上截距47.4147。由於月份的係數-2.4283是負數,這表示11月到12月間,月份越大、氣溫越低。這個結果符合我們對月份與氣溫的認知。
適用4月到10月的LM2 / For Apr. to Oct. : LM2
最後我們來看看LM2:
LM num: 2
temperature = 0.2922 * month + 22.1745將月份乘上0.2922,再加上截距22.1745,這就是四月到十月的氣溫預測值。跟LM1與LM3適用於冬季的線性模型相比,LM2的月份係數0.2922雖然也是表示月份越大、氣溫越高,但是月份的影響卻不如LM1跟LM3來的大。意思是四月到十月這段期間大多都很熱,截距就有22.1745度了。
非線性預測模型視覺化 / Model Visualization
上圖為LM1、LM2跟LM3畫成折線圖,並搭配原本月份與氣溫的散佈圖的整合結果。藍點為氣溫的實際值,紅點與紅線為3個線性模型的氣溫預測值。3月到4月、10月到11月之間沒有連線,這是因為他們適用於不同的模型。
比較實際值與預測模型之後,是不是更容易讓你解釋資料的變化了呢?M5P就是這麼好用啊。
比較不同演算法的預測能力 / A comparison of regression algorithms
M5P是一個白箱的演算法(white-box algorithm),它產生的預測模型容易讓人類解讀。儘管通常白箱演算法的預測能力並不如類神經網路(多層次感知機)與支持向量機等黑箱演算法來的準確,但M5P演算法可不一樣。在許多時候,M5P的預測能力可不會輸給其他黑箱演算法的喔。
以下就讓我們用月份與氣溫這份資料集,比較白箱演算法M5P、線性迴歸(LinearRegression)以及黑箱演算法的多層次感知機(MultilayerPerceptron)和支持向量機迴歸演算法(SMOreg)等不同迴歸演算法,它們平均標準誤的差異吧。
| 演算法 | 類型 | 平均標準誤 | 排名 |
| M5P | 白箱演算法 | 3.2438 | 1 |
| SMOreg | 黑箱演算法 | 4.5609 | 2 |
| LinearRegression | 白箱演算法 | 4.6148 | 3 |
| MultilayerPerceptron | 黑箱演算法 | 5.1554 | 4 |
從上表可以看到,M5P的平均標準誤為3.2438,比起非線性資料處理高手的支持向量機迴歸演算法SMOreg還要厲害呢。
結語 / Conclusion
深度學習的興起讓大家將目光一直放在正確率的提升上。正確率在實務應用上的確很重要,不過對研究者來說,預測模型的可解釋性其實更為有用。研究總是會希望透過分析所得到的模型來理解資料背後呈現的現象,但是深度學習、多層次感知機這種類神經網路,或是支持向量機等黑箱演算法所呈現的模型,往往對解讀資料沒有多大幫助。很多人會將之視為資料為非線性、難以摸清楚資料的模式,就放棄去理解原因,只著重在預測的正確率上。這在實務應用上還可以,但對追求真理的研究者來說,搞清楚為什麼造成這樣的原因,才是我們想要的結果。
因此,對於機器學習、資料探勘等分析方法,我一向比較注重的是模型的可解釋性。M5P能夠準確預測非線性的資料的同時,又能歸納出多種線性模型的規則,有助於資料的解讀,非常地好用。然而這個實用的演算法卻鮮為人知。
大多數資料探勘跟統計課程至多提到多元線性迴歸(也就是線性迴歸),以前我也寫過「以SPSS實作解釋型多元迴歸」的做法。在SPSS中提供了自變項影響程度的檢定,能夠讓我們確定該輸入資料的係數是否顯著影響預測結果。但線性迴歸很難處理非線性資料。雖然也有用二次項、三次項等曲線迴歸公式來建構非線性預測模型的方法,但是建構過程複雜且成效不彰,有些統計課本會介紹,但卻很少看人真的拿來用過。
相對的,M5P就能夠準確預測非線性資料。不過M5P沒有提供係數檢定或共性診斷等統計常用的分析方法,這就得有些取捨。
我試著依照M5P建構的模型樹,將資料拆解成不同的部分,例如1月到3月、4月到10月、11月與12月這樣分成三份資料,再到SPSS中去進行檢定分析看看。結果產生的三個迴歸模型跟M5P產生的略有不同,4月到10月的資料中月份的係數有達顯著,但其他的資料都是接近顯著(0.058跟0.067)。不過我這份資料過少,月份只有12個月,最後的氣溫卻是十分發散,不顯著也是合情合理啦。
最後我再補充一件事情,這篇所講的M5P跟線性迴歸都是在預測連續數值的依變項,像是分數、氣溫等資料類型。如果想要解釋的依變項是類別變項,那我建議大家使用關聯規則HotSpot演算法,這比起決策樹來說能夠發掘更多規則,有助於研究結果的詮釋。關於HotSpot的介紹,請看我之前寫過的「聚焦於你感興趣的關聯規則:Weka的HotSpot演算法」。
本篇對M5P的介紹就到此為止了。你用過機器學習、資料探勘中的那些迴歸演算法呢?你覺得M5P跟統計教的迴歸有什麼不同呢?你會使用M5P來分析什麼資料呢?如果有更好的白箱演算法,可以在下面留言處與我分享嗎?如果你覺得我這篇寫的不錯的話,請在AddThis分享工具按讚、將這篇分享到Facebook等社群媒體吧!感謝你的耐心閱讀,讓我們下一篇見。













請問Relative absolute error及Root relative squared error的%指標,要介於多少模型才能接受呢?
回覆刪除85-99%的範圍算好或不好?
謝謝。
To 自然,
刪除這沒有一定的答案
畢竟每個資料集的資料分佈不同,性質也差異很大
很難有一個絕對的標準
第一個做法是各別的線性迴歸模型拿去做輸入資料(自變項)對於輸出資料(依變項)的預測是否有顯著影響
就跟我在前面結語做的一樣
但這也不是很正規的做法
常見的做法是比較,又可以分成兩種
第一個是同樣的資料集,但採用不同的演算法去做比較,就跟我前面的「比較不同演算法的預測能力」做法一樣。這是工科研究常用的做法,但主要目的是評估演算法的優劣。
第二個是用同一個領域的代表性資料集,採用同樣的演算法來比較。
這個方式是沿用效度分析中的準則效度分析法
代表性資料集是那來作為比較的準則(效標),而你的資料集就是那來跟它做比較
這大概是我想到的做法
至於怎麽做比較好,可能還要找論文來看看