聚焦於你感興趣的關聯規則:Weka的HotSpot演算法 / Association Rule Mining with Specific Right-Hand-Side: HotSpot Algorithm in Weka
說到資料探勘(data mining),大部分的應用都是指購物籃分析(market basket analysis)中的關聯規則分析(association rule mining),也就是Apriori演算法。但傳統的Apriori有著許多限制:難以處理多維度資料、不能處理連續型的數值資料,最重要的是,研究者所感興趣的結果往往難以被探勘出來。後來我找到了另一種關聯規則分析演算法:HotSpot,它不僅可以解決上述Apriori所遭遇的問題,我還用AutoIT額外撰寫了資料整理的程式,使得HotSpot能夠呈現更多我們所關住的結果。
關聯規則分析的優缺點 / The Pros and Cons of Association Rule Mining
Apriori演算法可說是關聯規則分析的代表,其最常用的例子就是上圖中的購物籃分析。很多人會舉的例子「買尿布的人也會買啤酒」就是在指這個關聯規則分析 (雖然這只是個都市傳說)。曾經有段期間,關聯規則分析可說是資料探勘(data mining)的代名詞,但在實務上卻很少人能夠順利掌控關聯規則分析。直到今日,深度學習(deep learning)的興盛已經幾乎取代了資料探勘的內涵,關聯規則分析更是乏人問津。
到底是什麼原因造成Apriori為首的關聯規則分析沒落呢?除了Apriori演算法本身的限制之外,最主要的應該是關聯規則分析的理論背景跟現代使用者需求不合的關係吧。以下我就這兩點來跟大家聊一下關聯規則分析的優缺點。
Apriori演算法的限制 / Limitation of Apriori algorithm
我們先談談Apriori原始演算法的問題以及很久以前就已經有人提出的解決方法:
- 無法處理多維度資料:購物籃所買的東西是單一維度的資料。但是很多時候,我們會想要連同顧客的背景資料一起分析,這樣就是多維度資料處理的問題。若關聯規則包含二個維度以上的敘述,就稱為多維度關聯規則分析 (multi-dimensional association rules) 。其中,依照維度是否允許重複出現在關聯規則的差異,多維度關聯規則分析由可分為沒有重複出現的維度間關聯規則分析 (inter-dimensional association rules) 跟有重複出現的的混合維度關聯規則 (hybrid-dimensional association rules) 。
- 沒有辦法處理連續形態的資料:購物籃分析是針對「有買某件商品」來進行分析,屬於類別資料。如果要處理的是數值類型的資料,那麼可以應用資料離散化、裝箱法等做法,把連續資料轉換成類別資料,這樣就可以在Apriori中處理。這一系列的研究統稱為「數值式關聯規則分析 (quantitative association rules analysis)」。
- 沒有辦法聚焦於感興趣的關聯規則:雖然上圖的例子中我們可以發現「牛奶」跟「麵包」常常被一起購買,但很多時候經營者在意的是特定商品跟其他商品搭配購買的情況。像是最近毒蛋新聞喧囂直上,比起牛奶或麵包,我們更想知道「蛋」的關聯規則。為了讓使用者指定他所關注的關聯規則,許多關聯規則分析的系統打著「限制性關聯規則分析」的名號,將關聯規則結果以資料庫的方式呈現,讓使用者可以進一步篩選想要觀看的結果。
上述這一系列的相關研究大概都在兩千年以前就有很成熟的解決方案。而我這篇要介紹的HotSpot演算法,正是可以處理多維度、數值的連續資料、並且限定感興趣關聯規則的關聯規則分析技術。
不過,關聯規則分析的問題看起來大致上都已經克服了,為什麼關聯規則分析依然無法受到青睞呢?我思索已久,歸納出另一個觀點,下面繼續說明。
關聯規則分析的哲學背景:事後分析 / The philosophy of association rule mining: Post Hoc analysis
關聯規則分析是對既有的資料進行分析,找出資料之間隱含的關聯規則,用來幫助研究者推敲、探索存在於資料背後的原因。這種從事後結果來檢視現象的做法,可說是一種探索性分析(exploratory data analysis, EDA)方法。
相較之下,以深度學習為首的分類(classification)與迴歸(regression)則是著重於預測未知、協助人們進行決策的方式。雖然分類演算法也是使用大量的資料進行建模,但是這個建模是為了能夠用於後續的預測,這個建模並不是主要為了解釋資料本身。
顯然的,後者的做法符合現代的潮流:大家要的是一個明確的答案。關聯規則分析雖然可以找出很多關聯規則,但是卻只會讓經營者更加混亂、難以進行決策。關聯規則分析善於解釋既有的資料,但是卻不擅長預測未知的資料,我想這可能就是關聯規則分析逐漸沒落的原因吧。
然而,關聯規則分析的這種事後分析的特色,比起實務應用,更是適合作為研究分析的第一步。Lent等人(1997)認為分類演算法所建立的預測模型,著重於可從未曾見過的案例中預測其所屬的分類目標,但模型是否容易理解與解釋就不是分類演算法的主要考量。相反的,關聯規則分析的策略使用的是利用支持度找到最大涵蓋(covering)的規則,而非像分類中決策樹使用的切割(partitioning)策略 (Friedman & Fisher, 1999)。涵蓋與切割是資料探勘中長久以來爭辯的議題。Mitchell (1997)指出,相較於找尋彼此互斥的分割策略,由涵蓋策略歸納的規則具有更高的表達能力(expressive)。
舉例來說,我們手邊有大量的資料,但我們要怎麽著手開始分析呢?不同維度之間的資料有什麼關聯嗎?這些問題都可以用關聯規則分析來協助研究者進行分析。關聯規則分析本身也是一種不仰賴母體模型、容易理解的做法,因此不會像許多推論統計法容易受限於前提假設(但其實推論統計主要目的是驗證,並非探索,兩者本來就不能混為一談)。一旦找出有趣的關聯規則之後,研究者就能據此擬定假說,進一步設計實驗來驗證關聯規則分析所發現的現象。
HotSpot演算法介紹 / Introducation to HotSpot Algorithm
HotSpot演算法是Weka中需要另外安裝的HotSpot套件,而HotSpot套件是由Weka的核心開發者Mark Hall所維護。該套件參考Friedman與Fisher (1999)的PRIM資料分析演算法發展了HotSpot演算法。HotSpot演算法根據使用者所感興趣的目標項目來找尋最大化或最小化的一套樹狀結構規則,可於找尋類別類型與數值類型等各種資料類型的規則。在處理類別變項的時候,HotSpot演算法會在最小支持度的限制下找尋該類別出現機率較多的變項;而處理連續變項的時候,HotSpot則會找出大於整體平均數的規則。HotSpot演算法可以用於相當多場合,以醫療保險為例,研究者可以聚焦分析最高風險 (也就是死亡率最高) 的客戶群,最後可以找出他們共同出現的關聯規則分析結果為平均保險支出最多。(Hall, 2013)
Weka安裝HotSpot演算法 / Install HotSpot package in Weka
HotSpot套件需要透過Weka的Package Manger安裝,套件名稱是「hotSpot」(有時候真搞不懂Weka的大小寫規則)。Weka套件的安裝方法請見:「Weka下載與套件安裝教學」這一篇的介紹。
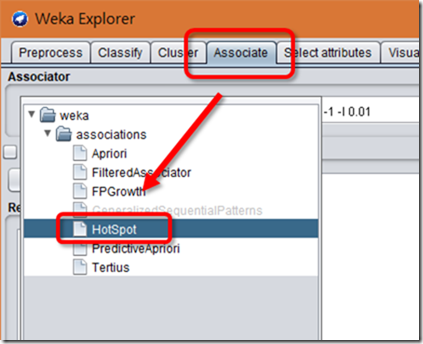
如果順利安裝的話,就可以在Weka的Explorer中的Associate (關聯規則分析)分頁中找到「HotSpot」演算法囉。
安裝Weka HotSpot Caller / Weka HotSpot Caller Setup
雖然我們可以在Weka Explorer裡面使用HotSpot,但因為內建的HotSpot一次只能分析一個感興趣的項目 (例如我想要分析「成績=高」與「成績=低」的學生,我就必須執行兩次),而且分析結果不太好閱讀,所以我用AutoIT做了一個操作Weka HotSpot的小程式,名為「Weka HotSpot Caller」。
- Weka HotSpot Caller程式碼保存庫:https://github.com/pulipulichen/weka-hotspot-caller
要使用Weka HotSpot Caller的話,必須要是Windows環境,然後參考「如何從GitHub下載檔案?」這篇的做法將程式碼下載到任意資料夾中。
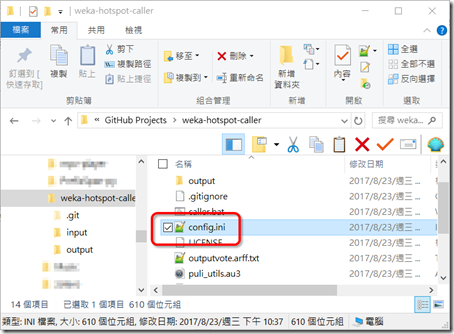
然後我們要修改它的設定檔「config.ini」。我建議使用Notepad++來修改。
其中我們需要調整的就是expapp_weka的參數,請按照你電腦中安裝Weka的位置來設定相對應的參數。如果你是安裝Weka 3.8版本,然後用預測安裝路徑安裝在C:\Program Files底下的話,你的Weka jar路徑應該就是上圖中的「C:\Program Files\Weka-3-8\weka.jar」。
我們也可以在檔案總管裡面看看Weka jar檔的實際位置,如上圖所示。這個做法是延自於「以AutoIT實作Weka預測執行檔」這篇。
使用Weka HotSpot Caller / Weka HotSpot Caller Usage
安裝好Weka中的HotSpot套件,並且配置好Weka HotSpot Caller之後,我們就要來使用HotSpot分析關聯規則囉。這個分析的操作步驟跟「循序樣式探勘:以Python的PrefixSpan實作」這篇很像,只有三個步驟。以下就讓我們來看看怎麼做吧。
1. 準備資料集 / Preparing data set
首先,我們要先準備一份資料集。這篇提出的範例是「score.csv」檔案,這是一份修課學生的學習資料與期末成績評等。老師想知道被評為「優等」跟「普通」的兩種學生各有什麼特質,就可以藉助HotSpot來進行分析。學生的學習資料包括「上線時間」、「所屬學院」跟「完成作業」三種。「上線時間」是已經編碼的連續資料,屬於順序尺度,1表示是「30分鐘以下」、2表示是「30分鐘至2小時之間」、3則表示是「2小時以上」;「所屬學院」是類別變項,分成「文學院」跟「理學院」;而「完成作業」與否則是布林變項,處理方式跟類別變項相同。
我也用「score.csv」這份檔案來說明HotSpot與Weka HotSpot Caller對資料上的要求:
- 目標屬性:最後一個欄位會被視為需要必須要出現在關聯規則分析結果項目集的目標屬性,也就是這個例子中的「期末評等」。在關聯分析中通常會將結果項目集稱為right-hand-side,縮寫為RHS。目標屬性必須是類別變項,不可以是連續變項。
- 其他屬性:除了最後一個欄位之外,其他的屬性皆會被視為可能出現在前提項目集 (left-hand-side, LHS)的來源,也就是這個例子中的「上線時間」、「所屬學院」跟「完成作業」。其他屬性可以是類別變項,HotSpot會找出所佔全體比例最高的項目;也可以是連續變項,HotSpot會找出平均最高的項目。
- 忽略特定項目與缺失值:若類別變項中有不想出現的項目,例如我只想找出「完成作業=是」,而不想要找出「完成作業=否」的話,只要將「完成作業」的「否」改成「?」,視為缺失值,HotSpot就會略過不分析。
接著將「score.csv」放到「input」資料夾中,我們就準備好可以開始分析囉。
2. 進行分析 / Start analyzing
接下來找到根目錄底下的「weka_hotspot.exe」,執行它。
接著會跳出一個AutoIT的提示視窗,這時候AutoIT正在操作Weka執行HotSpot演算法。AutoIT的做法請見「weka_hotspot.au3」這個檔案。
接下來需要等一段時間,因為AutoIT會連續執行多次HotSpot演算法,並且整合分析結果。提示視窗消失就代表分析完成。
3. 取得結果 / Get the result
當分析完成之後,我們就可以在output資料夾中找到「all_result.html」的分析結果。請用瀏覽器打開這個檔案。
我們可以看到分析結果中有兩個大表格。「score.csv (max)」的max表示是找尋符合多數情況的關聯規則。相對的,「score.csv (min)」的min就是找尋符合少數情況的關聯規則。以下我以「score.csv (max)」為例進行說明。
score.csv (max)
| RHS | LHS itemset | cover | conf | lift | lev | conv |
| 優等: 50% [5/10] | 所屬學院=文學院 | 5/7 | 71.43% | 1.43 | 0.15 | 1.17 |
| 完成作業=是 | 4/6 | 66.67% | 1.33 | 0.1 | 1 | |
| 上線時間 <= 1 | 3/5 | 60% | 1.2 | 0.05 | 0.83 | |
| 普通: 50% [5/10] | 所屬學院=理學院 | 3/3 | 100% | 2 | 0.15 | 1.5 |
| 完成作業=否 | 3/4 | 75% | 1.5 | 0.1 | 1 | |
| 上線時間 > 1 | 3/5 | 60% | 1.2 | 0.05 | 0.83 |
首先第一個欄位「RHS」表示我們要分析的目標屬性,分成「優等」跟「普通」兩種情況,各有5個案例。其中,期末評等為「優等」的學生通常具備了「所屬學院=文學院」(7位學生中有5位符合)、「完成作業=是」(6位學生中有4位)跟「上線時間<=1」(表示上線時間不到30分鐘,5位學生有3位符合);而期末評等為「普通」的學生通常具備了「所屬學院=理學院」、「完成作業=否」跟「上線時間 > 1」的關聯規則。
HotSpot演算法同時會計算多種評估關聯規則的指標,包括含括案例數(cover)、信賴度(conf)、增益度(lift)、槓桿度(lev)與肯定度(conv)。我們以RHS為「優等」、LHS為「所屬學院=文學院」這條關聯規則來說明這些指標的用意:
- 符合案例數(cover):前提項目集LHS發生的時候,結果項目集RHS也出現的個數。算法等同於信賴度。這個指標是我額外寫上去的,有助於解釋資料。
- 信賴度(Confidence,簡稱conf):測量了前提項目集LHS發生時,結果項目集RHS也出現的條件機率。信賴度71.43%是「所屬學院=文學院」的學生中,有71.43%的學生案例會是「期末評等=優等」。信賴度的計算方式如下所示:
- 增益度(Lift):此指標是由Silverstein、Brin與Motwani(1998)所提出,其目的是比較信賴度與結果項目集RHS單獨發生時的大小。增益值1.43即是考慮到信賴度為0.7143 (前面的71.43%),而結果項目RHS出現機率為0.5時,0.7143除以0.5得到的數值,表示此規則的信賴度比起結果項目集RHS單純的機率更高。增益度的計算方式如下所示:
- 槓桿度(Leverage,簡稱lev):此指標是由Piatetsky-Shapiro (1991)所提出,其目的是比較前提項目集LHS跟結果項目集RHS兩者同時出現的機率對兩者各別出現機率相乘的增加程度。槓桿度0.15表示學生同時符合期末成績為優等和所屬學院為文學院的機率,跟期末成績為優等的單獨機率、與所屬學院為文學院的單獨機率相乘結果相比,增加了15%的機率。槓桿度的計算方式如下所示:
- 肯定度(Conviction,簡稱conv):此指標由Brin等人(1997)所提出,用來表示前提項目集LHS與結果項目集RHS兩者相關的程度。如果肯定度為1,表示兩者並不相關。肯定度1.17表示此規則比起完全前提項目集LHS與結果項目集RHS在完全隨機組合的情況下出現機率更提高了117%。肯定度的計算方式如下所示:
值得一提的是,HotSpot也有最小支持度的設定,不過這個我已經預先寫在config.ini中的hotspot_support=0.01中,表示符合案例低於1%的關聯規則不納入結果中。由於HotSpot演算法會以信賴度、增益度、槓桿度、肯定度由高到低來進行排序,我們觀察分析結果時看前面幾個關聯規則就很容易找出令人感興趣的結果,最小支持度的過濾門檻就不是這麼重要了。
因此,透過以上分析,我們就能很快地找出「優等」跟「普通」學生所具備的特質。規則清楚且容易理解,算法簡單不複雜,是不是很不錯呢。
關注多重結果項目集 / Focus on Multi-RHS
上述的做法中,我們一次只能關注一種結果項目,像是「期末評等=優等」這樣的學生。如果我們想要的同時觀察符合「期末評等=優等」與「所屬學院=文學院」的學生,會符合什麼關聯規則時,我們可以調整輸入的資料集來達到這個目的。
我們先用試算表常具備的CONCATENATE 函數將「所屬學院」跟「期末評等」兩個欄位以「&」合併成一個欄位,就完成上圖的資料集。
再用同樣的方式進行分析。
這樣就可以得到考慮兩種維度資料的結果項目集RHS,再以此觀察你感興趣的RHS即可。舉例來說,我們可以看到同時是「文學院」與「優等」的學生,通常會出現「完成作業=是」跟「上線時間<=1」的關聯規則。
小結 / In closing
我們在分析資料的時候,除了研究著重的自變項與依變項之外,通常還會一併蒐集各種背景變項。但是面對大量且多維度的資料時,通常大家也只是分析驗證一開始提出的假設,大多資料都因為難以分析而被忽略。
這段時間以來,我一直在找尋更容易解釋資料的分析技術。我之前雖然寫過一篇「那個才是影響依變項最多的自變項?以SPSS實作解釋型多元迴歸」,但後來發現在資料維度太多、資料分佈不符合常態分佈的時候,多元迴歸通常無法跑出結果。後來我又幾經翻找,最後整理出來的就是這個HotSpot演算法。
(圖片來源:資料挖礦與大數據分析)
有些對資料探勘熟係的讀者可能發現到HotSpot演算法的結果跟粗糙集(rough set,或翻譯為約略集合)似乎很像,但後者會找出一個接近正確結果的逼近集範圍,而前者是明確的關聯規則。根本概念上還是有些不同。目前我只有看到R程式語言有粗糙集的分析法,詳情請看「資料挖礦與大數據分析」這本書的「第8章 約略集合理論」。
總而言之,HotSpot演算法不僅很適合作為研究分析的第一步、瞭解特定對象所具備的特質,還能夠協助研究者進行原因的診斷,用途相當廣泛。如果你蒐集好研究資料準備進行分析的話,不妨先使用HotSpot來看看資料本身有什麼隱含的關聯規則吧。













![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjLT2XOx2ebUFPrIMXOvYZyiXOJb_rUZWxgMyave7lD5XIRe3lnvmbBgvPXqcB62B6COCSdlv0HpMjJPMsSAEo9kjNcYQvT2sMq7TPqeLhNEmjlTmwGdwQedFw7VRjJgyHnN5mKHA/rw/?imgmax=800)
![clip_image002[8] clip_image002[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiESAAjwuRww11NjvTzfu5sXHpk2QefoAPFTK1Dl_hNRnnbHygmGVUMHNRiyJHjUURyz6VHa0aio6-jc37BeJYv4HdnpUdNogGLdb2viJkpOR-vAP-MXJRHxeb_lUjhYtVXuOXcMg/rw/?imgmax=800)




原來這種方法被稱為「限制性資料探勘」(contrast set mining)、「子群組發掘」(subgroup discovery),最後的統稱是「監督式敘述性規則歸納」(Supervised Descriptive Rule Induction, SDRI)
回覆刪除為甚麼weka_hotpot.exe一按下去就會停止運作QQ
回覆刪除To 鼎巳,
刪除我現在不太使用Weka的HotSpot,傾向於改用子群組探勘或特殊模式探勘。
關於特殊模式探勘,請用Cortana:
http://blog.pulipuli.info/2018/01/cortana-discovery-knowledge-in-your.html
後來再嘗試一下就能跑出結果了~
回覆刪除我是跨修資料探勘這門課的新手,對非本科系的人來說你寫的教學真的很讓人感動QQ,詳細易懂,救了期末報告~
To 鼎巳,
刪除喔喔,可以用就好。
喔對了,雖然我不太知道你們資料探勘在修什麼,不過HotSpot嚴格來說不太算是常見的關聯式規則探勘,兩者不太一樣喔。
目前學術界用HotSpot這種子群組探勘的人還蠻稀少的,我就很好奇你為何會來看我這篇?
本來是想用WEKA跑Aprori(有在課堂上介紹過的其中一種演算法)找關聯規則,結果發現竟然不能使用RRR
回覆刪除所以就上來找方法了~
嗯對,與其說是Weka的Apriori不能用。
刪除不如說Weka的Apriori所需要的資料格式跟結果,很多人都誤解了。
有興趣的話請去看「王者歸來 WEKA機器學習與大數據聖經」裡面的教學。
不過,關聯式規則本身就很難用。
目前看到的例子中,只有市場購物車跟網頁操作行為順序這種要在超級隨機的狀態下找到值得注意的關聯,才會使用關聯式規則。
不然大多情況下用關聯式規則都沒什麼意義,最多情況是你也不知道你自己在分析什麼。
雖然大家說資料探勘是由「分類」、「分群」、「關聯式規則」所組成。
「關聯式規則」的相關技術跟研究也非常多,但一般人其實是很難用它的。
您好,想請教兩個問題
回覆刪除1.除了目標屬性之外,其它屬性是否不能太多(我的data總共有97項),因我開始執行weka_hotspot.exe時出現error
2.我的資料除了有數值類型大部份以類別為主,但都已編碼為"0"或"1",是否是出現error的原因之一呢?
作者已經移除這則留言。
刪除To linlin,
刪除這樣很難說,我建議你用Weka的Explorer直接分析,不要用我另外寫的Weka HotSpot Caller,畢竟我額外寫的程式可能會有其他問題。
----------------
1. 關於能不能執行HotSpot的問題
我試了一個大型資料集
https://www.cs.ubc.ca/labs/beta/Projects/autoweka/datasets/
gisette.zip裡面的train.arff,檔案大小52.9MB,屬性數量5001個
使用HotSpot可以執行,耗時不到30秒
http://2.bp.blogspot.com/-5s6M64yxGKw/XVZ5Mw4K7KI/AAAAAAAEWwE/LWc5HzEgCxowdyJUQFHF8agEQsPwnTu8wCK4BGAYYCw/s1600/2019-08-16_172714.png
HotSpot執行參數是預設值
weka.associations.HotSpot -c last -V first -S 0.33 -M 2 -length -1 -I 0.01 -R
我的電腦是Intel i7-3770,RAM 16GB
你先試試看能不能分析這個檔案
-----------
2. 關於類別型屬性被編碼成數值的問題
可以在Preprcoess裡面用NumericToNominal,將數值型屬性轉換成類別型
Filter:
weka.filters.unsupervised.attribute.NumericToNominal
如果是以A, B, C之類的編碼,Weka一開始就會把它當作類別型屬性
但這件事情跟能不能執行HotSpot演算法應該關係不大
謝謝您~非常感謝!你的文章都寫得很仔細也很容易了解....非常受用!!
刪除To linlin,
刪除不客氣
借串詢問
刪除已經使用NumericToNominal這個程序,但還是不能使用Apriori
還可能是甚麼問題嗎?
謝謝你,簡單易懂
回覆刪除To eason,
刪除不客氣,能幫上忙就好。
作者已經移除這則留言。
回覆刪除To new,
回覆刪除關於Apriori的使用,我找到了YouTube上Krishma Punjabi的教學影片
https://www.youtube.com/watch?v=YxqIdh5Lzq0
她用的資料是The contact lenses database
https://archive.ics.uci.edu/ml/datasets/Lenses
我把資料轉換成試算表格式,你可以看看
https://docs.google.com/spreadsheets/d/1kdOc_rWn6nzUSKPFBr0n-TDqK8BB8AdgAvwWt2o-5Ss/edit?usp=sharing
裡面只能是nominal的類別類型而已
不能使用數值類型numeric
收到了,非常感謝
刪除To new,
刪除不客氣。
您好,不好意思,剛剛下載到輸入資料的過程都很順利,唯獨結果的部分跑不出來,頁面只有欄位但沒有任何數值等等出現,就連壓縮包裡的示範檔案的結果也是。想請問您是否有遇過此狀況呢?謝謝您
回覆刪除您好,
刪除請先直接使用HotSpot分析看看
https://lh3.googleusercontent.com/-zQU0Ab0Z0oY/X-jiVpxgPbI/AAAAAAAE3mQ/EWu8tvGBWno9nIxPAMzzukGUB7sZfMTfACLcBGAsYHQ/2020-12-28_033601.png
執行結果很正常
您好,Weka裡的Hotspot是可以開啟的,但檢視HotSpot Caller裡Inputy資料夾中的示範excel會是亂碼
刪除您好,
刪除因為Excel開啟CSV時接受Big5編碼,它不能接受比較通用的UTF-8編碼
請捨棄使用Excel,改使用LibreOffice Calc
https://blog.pulipuli.info/2016/04/libreoffice-portable-libreoffice.html
請問您會使用multisearch classifier 嗎?目前好像都找不太到在explorer介面使用的相關資料
回覆刪除To Fred,
刪除你是說Weka的擴充套件multisearch-weka-package嗎?
https://github.com/fracpete/multisearch-weka-package
https://lh3.googleusercontent.com/-ohREwZQc0mQ/YAVvtXR_DDI/AAAAAAAE45Q/g9RIj5NdsuAaoqnIP6mqUr1r-MC416j5gCLcBGAsYHQ/2021-01-15_053310.png
這個套件需要額外安裝,從Package Manager找到multisearch來安裝
使用時請根據它的Capabilities來選擇適合的資料:
````
CAPABILITIES
Class -- Date class, Numeric class
Attributes -- Binary attributes, Date attributes, Empty nominal attributes, Missing values, Nominal attributes, Numeric attributes, Unary attributes
Interfaces -- Randomizable
Additional
Minimum number of instances: 1
````
它的Class只能適用於日期跟連續數字
所以我用cpu.arff來作為輸入資料
https://github.com/tertiarycourses/Weka/blob/master/Weka%20datasets/cpu.arff
結果順利跑出來
MAE 39.657
MESE 70.0969
對比一下其他的演算法:
LinearRegression
Mean absolute error 41.0886
Root mean squared error 69.556
MultilayerPerceptron
Mean absolute error 41.5204
Root mean squared error 65.286
SMOreg
Mean absolute error 34.8638
Root mean squared error 78.5746
好像沒有特別令人驚豔的地方
為什麼會突然想用multisearch classifier呢?
作者已經移除這則留言。
回覆刪除有讀者詢問conf、lift、lev、conv四個評估指標的計算方式。
回覆刪除https://docs.google.com/presentation/d/1_TI_a13WhFUG_GglneVXIdYeTJAf3aq9hryPY5TeqFI/edit#slide=id.ge2b38f7437_8_720
關於conf、lift、lev、conv四個評估指標,我在「2. 看穿因果:熱點分析 - 2021」投影片裡面有介紹過。
這四種指標的基本都是混淆矩陣中LHS跟RHS的機率。
LHS是指前提規則,例如「所屬系所=台文所」。LHS的機率是在資料集中,符合該LHS的比例。
RHS是指後果規則,例如「是否有逾期記錄=是」。RHS的機率是在資料集中,符合該RHS的比例。
https://blogger.googleusercontent.com/img/a/AVvXsEhZILFyJ9OlSbluLnLG54JIkWCuhLbITvT3Hw7jwO0QvK7VYGPYrFSmaA1cJt0YW39FfT1g410FpQD40XmM6op4KuvxhNU-ccVdfl40eYjCRgCMtSfq0AJ3WUpQQbKFNbLFAUDMoMW52_8mTQo9B15MQm-2qzQizPXMy0WCY4D1ua_kT6vmw42aog
我們來計算lift看看。
https://blog.pulipuli.info/p/2021-nccu-lib.html
資料集來自「2021 資料探勘技術於 圖書館讀者資料分析與應用」的例子。
舉例來說,P(LHS)「所屬系所=台文所」的機率是(60/9479),P(RHS)「是否有逾期的記錄=是」的機率是(2219/9479)。
而這之中同時滿足前提與後果規則的比率P(LHS⋀RHS)的機率是(24/9479)
則lift則是(24/9479)/((60/9479)*(2219/9479))=1.71
結果跟Weka計算的一致。
建議讀者可以自行算算看,應該就可以確認怎麼算了。