1. 試分別用Prim's and Kruskal演算法畫出下圖最校展開樹(step by step)，並說明兩演算法的差異：

鄰接陣列(x代表兩點之間沒有邊)

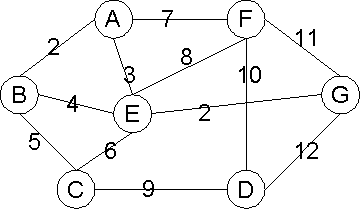
   A  B  C  D  E  F  G
 ┌                    ┐
A│0  2  x  x  3  7  x │
B│2  0  5  x  4  x  x │
C│x  5  0  9  6  x  x │
D│x  x  9  0  x  10 12│
E│3  4  6  x  0  8  15│
F│7  x  x  10 8  0  11│
G│x  x  x  12 15 11 0 │ 
 └                    ┘

2. 請利用Dijkstra's Alogorithm找出V0到其他頂點的最短路徑Shortest Paths(請詳列你的步驟及所用到的相關資料陣列)

鄰接陣列COST = ()
    V0 V1 V2 V3 V4 V5 V6
  ┌                    ┐
V0│0  1  4  5  ∞ ∞ ∞│
V1│1  0  ∞ 2  ∞ ∞ ∞│
V2│4  ∞ 0  4  ∞ 3  ∞│
V3│5  2  4  0  5  2  ∞│
V4│∞ ∞ ∞ 5  0  ∞ 6 │
V5│∞ ∞ 3  2  ∞ 0  4 │
V6│∞ ∞ ∞ ∞ 6  4  0 │
  └                    ┘

初值
DIST = [0 1 4 5 ∞ ∞ ∞]
PRIOR = [0 0 0 0 0 0 0]
Decides = [1 0 0 0 0 0 0]

DIST[W] > DIST[1] + COST[1][W]

請解釋上述符號及公式之意義，並試算之

3. 考慮下列四個矩陣相乘，說明你的演法如何求一個最佳解，使得相乘過程中使用的乘法數目最少(需列出Dynamic Programming的關係式與簡單的想法)

 　Ａ　 ╳ 　 Ｂ　 ╳ 　Ｃ　 ╳　 Ｄ
 20╳2       2╳30    30╳12    12╳18

4. 何謂0-1Knapsack Problem