社會網絡分析之隨機圖模型 / Social Network Analysis: Random Graph Models
這是介紹「PAJEK 蜘蛛: 社會網絡分析技術」這本書中的第13章「隨機圖模型」的投影片。這本書使用社會網絡分析工具「pajek 蜘蛛」來分析研究者所蒐集的實測社群本身可能符合或不符合那些隨機圖模型(random graph models)。書中介紹的隨機圖模型包括伯努利隨機圖模型(Bernoulli random graph model)、條件統一隨機圖模型 (Conditional uniform random graph models)、小世界模型 (small world model)與優先連接模型 (scale free model),它們有各自的假設背景、建構網絡的隨機過程以及展現出來結構特徵。本書以蒙特卡洛模擬(Monte Carlo simulation)來建構各個隨機圖模型的信賴區間,藉以判斷實測網路與這些隨機圖模型的異同。
投影片 / Slide
- Google投影片:第13章 隨機圖模型 (PDF、Power Point)
大綱 / Outline
- 為什麼要研究隨機圖?系統性效應
- 描述網絡(圖)的結構特徵
- 隨機圖模型
- 實測網絡最符合那個隨機圖?蒙特卡洛模擬
- 蒙特卡洛模擬練習
社會網絡的結構特徵 / Model features of a social network
本章作為該書的最後一章,用到了大量前面章節介紹過的各種描述社會網絡的指標。我在投影片裡面有整理各個指標與使用Pajek計算的操作方式,也順便在這裡條列一下,至於詳細的理論跟公式則需要回頭看書中其他章節,或是參考Pajek的操作手冊:
點度與組元 / Degree and Components
平均點度 (Average Degree)
點度是指一個頂點擁有的連線數量。 平均點度是指所有頂點的點度的平均值。
- [MAIN:MENU] Info > Network > General (Average Degree)
組元數 (Number of components) 與 最大組元規模(%) (Size of the largest component)
(弱)組元是最大的(弱)聯通子網路,不計方向。
- [MAIN:MENU] Net > Components > Weak
-
- Number of components
- Size of the largest component (proportion)
距離 / Distance
直徑 (Diameter)
網絡中最長的測地線(兩頂點之間的最短距離)
平均距離 (Average Path Distance)
距離(測地線)是指任兩頂點之間的最短距離。網絡中所有距離的平均數即為平均距離。
直徑和平均距離的操作如下:
- [MAIN:MENU] Net > Paths between 2 vertices > Distribution of Distances > From All Vertices
-
- Diameters 直徑
- Average path lengths 平均距離
傳遞性 / Transitivity
雲集係數(傳遞性) (Network Clustering Coefficient)
所有閉合性雙途徑在網絡中所佔的比例。
途徑(path):一種路線,在它的起始頂點和終末頂點之間,同一個頂點僅出現一次。
循環(cycle):一條閉合性途徑。
- [MAIN:MENU] Net > Vector > Clustering > CC1
-
- Network Clustering Coefficient (Transitivities)
中心勢分析 / Centrality
點度中心勢 (Degree centrality)
點度中心度用於頂點,等同於頂點的點度(degree)。 點度中心勢就是把現有網路的實際點度變異值,除以相同規模的網絡可能出現的最大點度變異值,所得到的比值。
- [MAIN:MENU] Partitions > Degree > All
中介中心勢 (Betweenness centrality)
中介中心度用於頂點,是指網絡中所有其他頂點之間的測地線中,經過該頂點的測地線所佔的比例。 中介中心勢用於網絡,是指把這個網絡的實際中介中心度變異值,除以相同規模的網路可能出現的最大中介中心度變異值,所得到的比值。
- [MAIN:MENU] Net > Vector > Centrality > Betweenness
接近中心勢 (Closeness centrality)
接近中心度用於頂點,是指其他頂點數除以該頂點與其他頂點的距離之和。 接近中心勢用於網絡,是指把現有網絡的實際接近中心度變異值,除以相同規模的網絡可能出現的最大接近中心度變異值,所得到的比值。僅能用於強聯通網絡(有向網絡)。
- [MAIN:MENU] Net > Vector > Centrality > Closeness > All
本征矢量(特徵向量)中心度 (Hubs-Authorities)
特徵向量中心度用於頂點,是指它與具有高度特徵向量中心度的頂點相連的程度。特徵向量中心勢用於網路,是指網路的實際特徵向量中心度變異值,除以相同規模的網路可能出現的最大特徵向量中心度變異值,所得到的比值。 (好像不能用於只有頂點跟連線的圖)
- [MAIN:MENU] Net > Vector > Important Vertices > 1-Mode: Hubs-Authorities
三方譜分析 / Triadic Census
003:三頂點不相連
102:雙頂點互通,一頂點不相連
201:A<->B<->C,但AC不相連
300:完全相連
- [MAIN:MENU] Info > Network > Triadic Census
隨機圖模型 / Random graph models
我在投影片裡面也有整理各個隨機圖模型的假說跟操作步驟,但這邊也列一下:
伯努利隨機圖模型 (Bernoulli random graph model)
假設所有的行動者都有可能平等地參與連線關係、行動者並不在乎他們與誰相連。
- [MENU] Net > Random Networks > Bernoulli/Poisson > Undirected > General
-
- 頂點數量:10
- 平均點度:1
條件統一隨機圖模型 (Conditional uniform random graph models)
假設是即使整體網絡存在限制條件,但行動者仍然是隨機地分派他們的連線。
- [MENU] Net > Random Networks > Vertices Output Degree
-
- 頂點數量:10
- 最小連線數量:0
- 最大連線數量:1
- 網路沒有多重連線嗎:是
(產生出的是有向網路)
小世界模型 (Small world model)
假設行動者傾向於與他們的鄰點的鄰點建立連線、行動者更偏好形成傳遞性閉合 (transitive closure)(可能是因為受限於地理位置、機構單位、興趣愛好),而這個傳遞性暗示了社會背景會影響社會紐帶的形成。
- [MENU] Net > Random Networks > Small World
-
- 頂點數量:10
- 鄰點數量:2
- 重連比例:0.5
優先連接模型 (Scale free model)
假設 行動者更傾向於與公眾人數建立關聯:如果許多人都認識某人,那麼我也就更有可能認識這個人 (馬太效應:富者越富、成功者更成功)。 反映出了社會機制中存在著推薦指標:人們進行選擇的時候會參考別人對某種事物或某個任務的選擇,並繼而強化這個事物或人物的受歡迎程度。 長尾效應:若實測網絡會長久保留讓後者可以看到,那麼它會相當符合優先連接模型的情況,例如blog網頁的連結、論文引用。
- [MENU] Net > Random Networks > Scale Free > Undirected
-
- 輸入頂點數量:10
- 輸入連線數量:0 (不限制)
- 平均點度:5
- 起始頂點:3
- 連線機率:0.7
- Alpha:0.3 偏向優先法
小結 / In closing
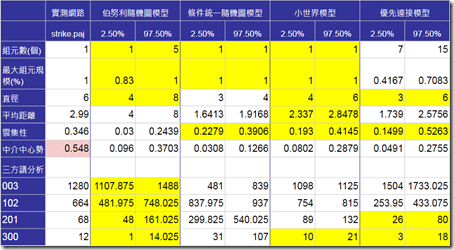
很遺憾的是,這一章我並沒能完全掌握。書中提及許多針對隨機圖模型的研究,也發掘出隨機圖模型的眾多特徵,但這些特徵伴隨著大量的數學公式與前面章節介紹過的各種概念,導致讀起來其實很辛苦。為了整理這份投影片,我又把整本書從頭到尾翻了好幾次,可真的是總複習的感覺。
另一方面,本章使用的蒙特卡洛模擬也是個大問題。書中使用的例子是有1490個頂點的部落格超連結社會網絡資料,而蒙特卡洛則需要為4種隨機圖模型、5類特徵重複運算1000次。我光是算平均距離就算到電腦快當機,索性另外找了比較小型的伐木工資料來作練習。
但是在操作的過程中也遭遇到很多問題。條件統一隨機圖模型跟優先連接模型的參數設定,書中並沒有講述完整的細節。特別是優先連接模型,只要連線機率跟Alpha參數設錯,Pajek就無法產生隨機圖。因此換個例子之後也不能完全照書上的做法來操作,投影片中的例子是我實際嘗試後的可行做法。
而最後產生的蒙特卡洛信賴區間在解釋上也有點含糊。這可能要參考更多論文,看看其他論文都怎麼用這種做法來解釋實測網絡跟隨機圖模型之間的關係吧。
總之,雖然還不能完全掌握隨機圖模型,不過這篇就先整理到這邊吧。












有網友在問我這篇的投影片怎麽下載。
回覆刪除投影片下載方法可以參考「如何下載「布丁布丁吃什麼?」的Google Docs投影片」這篇的教學
http://blog.pulipuli.info/2013/03/google-docs-guide-for-downloading-slide.html
或是直接從上面的投影片下方的連結Power Point下載連結中取得投影片檔案即可
作者已經移除這則留言。
回覆刪除作者已經移除這則留言。
刪除三方譜分析的操作為:
刪除[MAIN:MENU] Info > Network > Triadic Census
Pajek版本不太一樣可能操作會不太一樣