機器學習模型真的準嗎?從虛無假設檢定來檢驗模型成效 / Applying Null-Hypothesis Statistical Testing on Machine Learning Model Evaluation
這是我在2022年整理的文章「機器學習模型真的準嗎?從虛無假設檢定來檢驗模型成效」,現在在這個blog備份一下。
前言 / Background
隨著人工智慧的普及與日常化,利用機器學習演算法建立模型,並以模型進行預測,已經被很多人融入日常工作之中。建立模型本身不難,建立完成後我們也會用正確率或F-measure來評估模型,讓我們能掌握模型的預測能力高低。
一個機器學習模型是否可靠,我們通常會用各種評估指標來描述它。最常見也是最基本的評估指標就是「正確率」(accuracy)。將建立好的機器學習模型拿去預測測試集(test set),如果預測正確的比例是70%,那麼就會得到「正確率70%」的模型評估結果。當然,如果能夠100%正確,那的確是再好不過的事情,但大多時候機器學習模型的預測率都只能做到儘可能準確,100%正確率反而有點像是過擬合的結果。
然而,很多人會對「正確率70%」這樣的結果表示疑惑。「這個模型準嗎?該不會是剛好它猜中而已吧?」事實上,還真的會有與其用模型來進行預測的結果,甚至不如用佔比最高的類別來瞎猜的情況。
證實機器學習模型是否有比瞎猜還有準確,其實是有科學方法可以用來證實,那就是推論統計中的虛無假設檢定(Null-Hypothesis Statistical Testing)。也許有同學已經知道科學實驗或問卷調查會用到虛無假設檢定,但在機器學習評估模型上用虛無假設檢定來評估成效的做法,可能就不是這麼廣為人知了。
這篇文章將基於Japkowicz跟Shah提出的交互驗證t檢定(cross-validated t test),用有別以往的方式來評估機器學習的模型。文章最後也會介紹使用交互驗證t檢定的限制,以及其他用推論統計評估機器學習模型的方法。
你所知道的機器學習模型預測正確率 / How to evaluate a machine learning model?
在機器學習與資料探勘百科全書(Sammut & Webb, 2017)的定義中,「正確率」的意思是「模型的預測與被建模的資料實際符合的程度」。正確率通常以百分比來呈現,介於0%到100%之間。0%表示模型完全預測錯誤,100%表示模型預測完全正確。
接下來我們用德國人信用卡記錄資料集(Hofmann, 2000)為例子,利用Weka的J48決策樹演算法來建立模型,看看該模型的正確率評估結果。J48是源自Quinlan (1993)發表的C4.5決策樹演算法。J48不僅能夠將連續數值的屬性分割成決策樹的規則,也會對決策樹進行修剪,以達到簡化規則以及降低過擬合(overfitting)的可能性。
圖1 以訓練集評估J48建立的模型
德國人信用卡記錄資料集已經預先收錄在Weka中。資料集的檔案名字是「credit-g.arff」。首先我們用訓練集(training set)來評估J48模型的正確率,如圖1所示,得到的結果會是85.5%。然而,由於訓練集的資料皆是模型的已知案例,模型只是在本來就知道的結果下去進行預測,這使得訓練集評估模型的結果往往會過度樂觀。換句話說,85.5%的正確率很可能只適用於這份資料集,不一定適合未來的未知案例。
為了避免上述問題,模型的評估可以採用交互驗證(cross-validation)進行。交互驗證的做法是將資料集分成k個子集。每個子集作為測試集,而子集之外的其他案例則是作為建立模型用的訓練集。整個交互驗證的流程會進行k次的建模與驗證,k次的正確率取平均後即是交互驗證的最終正確率。而交互驗證的次數稱做「層」(fold)。交互驗證的層數常見是10層,這也是Weka預設的評估模型方式。
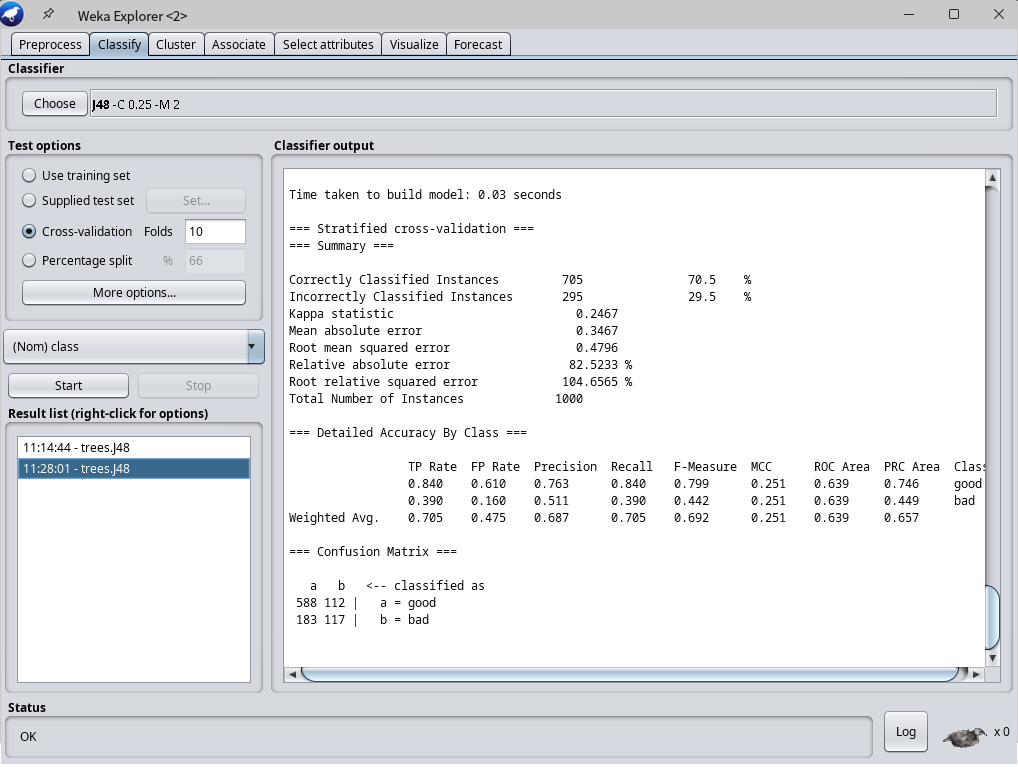
圖2 以交互驗證評估J48建立的模型
接著我們以交互驗證10層來評估J48模型,如圖2所示,10層評估結果平均正確率僅為70.5%。跟用訓練集評估相比,交互驗證的結果正確率低了很多,但這個評估結果會被視為較為貼近真實狀況的可信評估。
那麼我們回到一開始的問題,我們用J48建立的模型在交互驗證10層驗證下得到平均正確率「70.5%」,「這個模型夠準嗎?」一般來說,當資料集涵蓋了人為主觀判斷而自然產生的時候,由於人們判斷本身就有落差,導致模型的正確率通常也不會太高。舉例來說,Ahmed等人(2017)在製作用於情感分析的資料集時,請三位評分者將文本分類為「正面」、「中立」與「負面」,結果分類完全一致的比例僅有62.5%。
從這個角度來看,我們可以將既有的資料集視為是一位人類評分者給出的答案,而機器學習模型預測的結果視為另一位評分者,兩者分類一致的比例則是正確率。那麼前面J48演算法建立的模型得到「70.5%」正確率,似乎不算太差?
比較模型正確率的基準線 / The baseline of model evaluation
對於「這個模型夠準嗎」的問題,我們可以把它轉換成「這個模型預測的分類結果,比起直接猜還要來得準嗎?」為了回答這個問題,我們必須先定義什麼叫做「直接猜」,也就是跟模型比較的基準線。
用來表示基準線的方式可歸類為兩種不同的機率模型:零階模型(zero order model)以及一階模型(first order model)。零階模型又稱為等機率模型,是假設每種分類類別都會以同等機率出現。一階模型則是以現有資料的分佈作為機率模型。
我們用德國人信用卡記錄資料集為例子來說明零階模型與一階模型的呈現方式。信用卡記錄目標類別為「class」,類別有兩個種類:「good」跟「bad」,用來表示這個人的信用程度。零階模型認為每種類別出現的機率都一樣,也就是「good」可能出現的機率跟「bad」一樣,都是100% / 2 = 50%。如果以零階模型作為基準線,我們預測所有案例都是其中一種分類,那麼預測正確率會是50%,而這就是零階模型的基準線。
圖3 德國人信用卡記錄資料集的class分佈
一階模型則是將資料的實際分佈作為機率模型。德國人信用卡記錄資料集涵蓋的1000筆案例中,其中700筆被分類為「good」,另外300筆被分類為「bad」。相較於零階模型的平均機率分佈,一階模型顯然比較符合資料的實際狀況。如果是以一階模型作為基準線,我們用比例最高的類別來直接猜,以此作為預測結果,則預測正確率將會是700/1000 = 70%。
用一階模型作為基準線所得到的正確率70%來看,前面用J48演算法建置的機器學習模型得到的70.5%正確率,似乎也沒有比較準?這時候可能會有人主張,機器學習模型得到的70.5%正確率,還是比一階模型基準線還多上了0.5%,仍然有它存在價值。
然而,這個0.5%的差距,會不會是偶然的情況下、碰巧得到的結果呢?要回答這個問題,我們就得引入虛無假設檢定的概念了。
虛無假設檢定 / Null-Hypothesis Statistical Testing
虛無假設檢定(Null Hypothesis Statistical Testing)是推論統計中的核心概念。虛無假設(null hypothesis)是指大多時候都會發生的狀態,也就是上述的基準線。站在虛無假設的對立面,也就是機器學習模型的預測正確率高於基準線的假設,就稱之為對立假設(alternative hypothesis)。透過推論統計檢定計算,我們可以得到機器學習模型預測結果超越基準線的機率。當機率足夠大的時候,我們就能相信機器學習模型的預測正確率顯著地超越了基準線。
綜合以上所述,將基準線的正確率以μ0表示,而機器學習模型得到的正確率則用μx表示,我們可以將虛無假設H0和對立假設H1用以下兩種陳述句來表示:
當虛無假設與對立假設的陳述句確定之後,我們就能根據變項的資料類型,選擇合適的推論統計檢定方式,以此用來評估機器學習模型的正確率大於基準線0.5%的這件事情,到底是確實可靠的證據,還是偶然發生的結果。
交互驗證t檢定 / Cross-validated T test
將推論統計檢定應用到機器學習模型評估成效的做法中,Japkowicz與Shah (2011)認為最有統計效力的檢定方式是交互驗證t檢定(cross-validated t test)。顧名思義,交互驗證t檢定是先為機器學習模型進行10層的交互驗證。將每一層的評估結果視為從母體中的抽樣,再進行t檢定計算對立假設推翻虛無假設的機率,以此判斷對立假設的出現,到底是顯著的證據,還是無法拒絕虛無假設的偶然結果。
在檢定機器學習的模型正確率有沒有顯著大於基準線之前,我們要先來看看機器學習模型在交互驗證中各層得到的正確率。前面我們採用交互驗證10層是進行10次建模、計算各層正確率,最後得到平均正確率為70.5%。交互驗證每一層的正確率如表1所示,每一層正確率可視為對母體抽樣的結果。正確率介於64%到76%之間,標準差為3.6,平均值為70.5%。跟基準線70%相比,10層正確率中就有4層低於基準線,這已經開始讓人對J48演算法建構的機器學習模型抱持懷疑的態度。
表1 以交互驗證10層評估J48建立的模型
| 交互驗證各層正確率 |
| 72% |
| 64% |
| 68% |
| 70% |
| 72% |
| 69% |
| 73% |
| 67% |
| 76% |
| 74% |
再來我們要進行虛無假設檢定中的推論統計檢定。推論統計檢定必須依據待檢定變項的資料類型來選擇。我們要檢定的是機器學習模型交互驗證10層得到的正確率平均值是否顯著大於基準線,屬於單連續變項平均數單尾檢定的範疇。本次使用的德國人信用卡記錄資料集僅有1000筆,本身也是從全部德國人母體抽樣的結果。我們保守地將母體標準差視為未知,改用樣本標準差來推估母體標準差。因此最終選擇的推論統計檢定是單一樣本t檢定(one sample t-test)。
單一樣本t檢定是為樣本大小為n的樣本測量其X變項,計算出觀察平均數x̄obt與標準差sobt,以此計算該樣本平均數的觀察t值 tobt 。對照自由度為n-1的t分配,我們可以得到機率值p值。p值表示比觀察t值 tobt 或更極端的t值的機率。當機率值p值低到一種程度的時候,表示 tobt 已經足夠極端與異常,與一般情況下都會發生的虛無假設有顯著的不同,我們可以將之視為有信心去拒絕虛無假設。多少程度是用顯著水準α表示,目前普遍採用的顯著水準α為0.05。
再來我們以上面機器學習模型交互驗證結果來進行單一樣本t檢定。觀察t值 tobt 的計算公式與結果如下:
交互驗證10層表示樣本數n為10。其中一個樣本需用於推估母體標準差,自由度df則是9。接著我們就可以來查查看統計學家為不同樣本規模歸納的t分佈表格,得知t分佈中自由度df=9以及單尾檢定顯著水準α=0.05的門檻值為1.833。觀察t值 tobt 的0.44遠遠未達門檻值,表示機器學習模型的正確率並沒有足夠大到讓我們有信心推翻虛無假設。換句話說,機器學習模型的正確率70.5%剛好比基準線多0.5%的結果,只能說是偶然碰巧發生。
圖4 用PSPP進行單一樣本t檢定
除了手動計算查表之外,單一樣本t檢定的計算也可以用開源軟體PSPP來簡單完成。圖4是單一樣本t檢定的計算結果。其中顯著程度Sig.是即是前述的機率值p值,只是該處的p值是以比較有無差異的雙尾檢定(2-tailed test)來進行計算。如果我們要進行的是比較大或小的單尾檢定(one-tailed test),則需將此值除以2,以此得到p值為0.336。p值0.336沒有低於顯著水準α=0.05,依然表示機器學習模型得到的正確率跟基準線並沒有很明顯的差異。因此,面對「這個模型準嗎?該不會是剛好它猜中而已吧」的問題時,我們也只能說:「這個模型很可能只是剛好猜中而已,並沒有特別準。」
瞭解了使用J48演算法建置模型並沒有預測的特別準之後,我們換一個分類演算法,用樸素貝氏分類器(Naive Bayes)來建立模型,看看它的正確率有沒有比基準線還要好。在10層交互驗證之後,樸素貝氏的平均正確率得到了75.4%。乍看之下J48演算法的70.5%和樸素貝氏的75.4%好像並沒有多大差別,但在經過上述的交互驗證t檢定計算之後,可得出機率值p值為0.03,低於顯著水準α=0.05,表示樸素貝氏分類器模型正確率超過基準線的這件事情,並不是偶然碰巧的結果,而是讓人有足夠信心去相信的證據。
前提假設與限制 / Hypothesis and limitation
交互驗證t檢定可以應用於大多機器學習建立模型評估成效的情境,但使用前仍需注意交互驗證t檢定的前提假設與限制。這些自t檢定自身特性的前提假設如下:
- 抽樣結果為常態分佈或近似常態分佈:根據中央極限定理,以超過300個案例的資料集進行交互驗證10層即可符合此前提假設。詳細推論還請參照Japkowicz與Shah (2011)書中的論述。
- 隨機抽樣:需確保資料集來源為隨機抽樣。
- 母體變異數具有同質性:由於母體資料集的變異數未知,我們在此只能假設它並沒有違反此一前提假設。
除了上述的t檢定前提假設之外,本文採用的一階模型作為基準線評估方式,也會受到一階模型自身特性的限制。當資料集為不平衡資料(imbalance data)、案例分類的分佈相當極端的時候,佔比最高的分類會成為非常高的基準線。在詐欺偵測或是化學資訊學等實際應用中,不平衡的比例甚至會到1:1000或1:5000,此時的基準線就已經超過99%。機器學習模型要如何顯著比99%還要高,成為了相當難以克服的一大挑戰。
另一方面,當資料集的分類比例過於平均的時候,基準線大多也不會超過50%。此時虛無假設檢定過於容易被推翻,大多數機器學習模型的預測能力都能夠比直接猜還準,使得虛無假設檢定看起來有點多此一舉。
比較演算法的其他推論統計檢定方法 / Methods of Null-Hypothesis Statistical Testing
話說回來,我們知道J48演算法建置模型的正確率並沒有明顯超過基準線,而使用樸素貝氏演算法建置的模型則有顯著超越基準線,那我們是否可以認為樸素貝氏演算法的表現比J48演算法還要好呢?要回答這個問題,我們依然可以用虛無假設檢定來進行驗證。
圖5 對應不同機器學習問題使用的推論統計檢定方法
根據要比較的演算法數量(2個或多個),以及比較的資料集數量(同一份、多份)的不同情況,Japkowicz與Shah (2011)歸納了對應使用的推論統計檢定方法。如圖5所示,這些推論統計檢定方法橫跨了有母數與無母數的領域,包括了相依樣本t檢定(two-matched-samples t test)、麥可尼馬爾檢定(McNemar's test)、相依樣本維爾卡森符號檢定(Wilcoxon's signed-rank test for matched pairs)、符號檢定(sign test)、相依樣本單因子變異數分析(repeated measure one-way ANOVA)和弗里德曼檢驗(Friedman's test)及其事後檢定方法。根據情況的差異,虛無假設檢定的前提假設、虛無假設與對立假設的制訂細節也都有所不同。
如果我們想要比較J48演算法跟樸素貝氏演算法在同一份資料集上的正確率是否有顯著差異,此時就可使用相依樣本t檢定來評估,最後結果是樸素貝氏演算法的正確率有顯著超越J48演算法。至於詳細做法,還請查閱Japkowicz與Shah (2011)書中的介紹囉。
結語:機器學習模型有必要做推論統計檢定嗎? / Conclusion: Should we require Null-Hypothesis Statistical Testing to evaluate a model?
事實上,目前人工智慧與機器學習領域中,用推論統計檢定模型成效的研究並不常見。除了少部分研究者誤解了虛無假設檢定的用途之外,造成虛無假設檢定在學術領域盛行的較為少見的原因,可能可以從2006年Drummond的主張看到些端倪。他認為虛無假設檢定僅是評估方法的其中一種,而學術界應接受開放、多元的評估方式,而非被虛無假設檢定侷限了可能性。Demšar (2008)也認為網際網路資訊迅速發展的時代下,科學研究應更佳鼓勵探索與創新的方法。
儘管虛無假設檢定有各種前提與限制,Japkowicz和Shah (2011)還是認為虛無假設檢定在證實模型的成效上,仍然具有不可忽視的價值。至少,當有人質疑你建立的機器學習模型是否真的夠準的時候,不妨用虛無假設檢定來回答他吧。
參考文獻 / Reference
邱皓政(2005)。統計原理與分析技術:SPSS中文視窗版操作實務詳析。
- Ahmed, T., Bosu, A., Iqbal, A., & Rahimi, S. (2017). SentiCR: a customized sentiment analysis tool for code review interactions. In 2017 32nd IEEE/ACM International Conference on Automated Software Engineering (ASE) (pp. 106-111). IEEE.
- Demšar, J. (2008). On the appropriateness of statistical tests in machine learning. In Workshop on Evaluation Methods for Machine Learning in conjunction with ICML (p. 65). Citeseer.
- Drummond, C. (2006). Machine learning as an experimental science (revisited). In AAAI workshop on evaluation methods for machine learning (pp. 1-5).
- Japkowicz, N., & Shah, M. (2011). Evaluating Learning Algorithms: A Classification Perspective. Cambridge University Press.
- Quinlan, J. R. (1993). C4.5: programs for machine learning. San Mateo, Calif.: Morgan Kaufmann Publishers.
- Sammut, C., & Webb, G. I. (2017). Encyclopedia of machine learning and data mining. Retrieved from http://dx.doi.org/10.1007/978-1-4899-7687-1
那最後還是來問問大家一些問題吧。
你是怎麼評估機器學習模型的成效呢?








修正一些打字錯誤。
回覆刪除我還真的蠻喜歡這篇的,可以回答超多人的問題。