行為順序檢定:滯後序列分析 / Behavior Analysis: Lag Sequential Analysis
這是巨量資料探勘與統計應用課程的投影片「行為順序檢定:序列分析」。本單元是屬於系列課程中的「資料檢定級」的最後一個單元,處理資料類型也是在行為的「類別」類型資料,使用的分析技術就是以前我常常提到的滯後序列探勘(lag sequential analysis)。滯後序列分析是延伸前一單元列聯表的檢定方式,但是不像卡方統計量是用於檢定整體列聯表,它使用Allison與Liker(1982)的調整後殘差計算方式來做細格檢定。雖然資料類型都以列聯表呈現,不過計算方法可是差很多的喔。跟以前我介紹滯後序列分析的內容相比,這次不僅採用比較嚴謹的Allison與Liker的計算方法,還加入了相關係數Yule'Q的計算,並直接用jsPlumb畫出了事件轉移圖。本單元使用我所開發的滯後序列分析計算器來作計算,包含兩個實作學習單跟一份測驗,供同學邊看邊練習。
單元大綱 / Outline
- 行為序列資料表
- 滯後序列分析
- 滯後序列分析:樣本統計量 事件轉移表
- 滯後序列分析:檢定統計量 調整後的殘差
- 實作:序列分析
- 深入探討序列分析
- 課堂練習:幼兒平行遊戲行為研究
- 序列分析的應用
投影片 / Slide
- 教學投影片: Google Presentation
- 教學投影片其他格式: Power Point、 PDF、 OpenDocument Presnetation
我以Google簡報的檔案匯出成PPTX,再備份到以下位置:
- SlideShare 、 GitHub 、 OneDrive 、 Box 、 Mega 、 MediaFire 、 Google Drive
結論寫作框架 / Result Framework
請參考以下結論框架,將底線的文字改為合適的內容,完成滯後序列分析的結論吧。
| 研究目的 | ||||
| 本研究使用序列分析來檢定(研究對象)的行為序列資料中(寫出每一個事件「編碼」)之間是否有顯著轉移。 | ||||
| 樣本敘述統計量 | ||||
| 研究對象共(研究對象數量)位,事件總數為(事件總數)次。 (每個事件編碼都寫一次)
雙事件轉移序列總數為(序列總數)次。 | ||||
| 序列分析結果 | ||||
| ||||
| 事件轉移圖 (如果整體統計檢定達到顯著才寫) | ||||
| (可截取序列分析計算器的事件轉移圖) |
舉例來說,像是:
| 研究目的 | ||
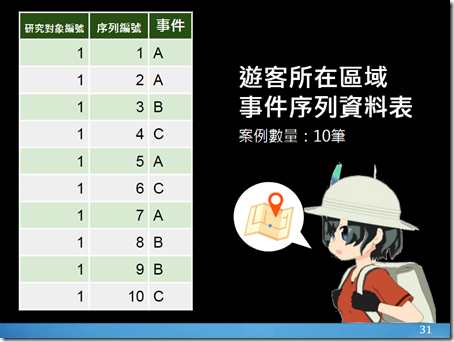
| 本研究使用序列分析來檢定遊客的行為序列資料中事件「A 熱帶莽原區」、事件「B 叢林區」與事件「C 沙漠區」之間是否有顯著轉移。 | ||
| 樣本敘述統計量 | ||
| 研究對象共1位,事件總數為10次。
雙事件轉移序列總數為9次。 | ||
| 序列分析結果 | ||
| ||
| 事件轉移圖 (如果整體統計檢定達到顯著才寫) | ||
學習單 / Worksheets
本單元包含了以下的學習單,請搭配課程投影片一起練習吧。
測驗 / Examine
本單元整理了一份測驗,供同學驗證所學:
資料集 / Dataset
本單元用到了以下資料:
- 遊客所在區域事件序列資料表:我自己編撰的例子。
- 幼兒平行遊戲事件序列資料表:這個例子來自Bakeman跟Gottman所著的「Observing interaction: an introduction to sequential analysis」。我之前的序列分析介紹也是用這個例子。
- 讀者瀏覽網頁行為序列:修改自孫賢潔所著的「行動政府網頁設計準則影響資訊尋求之研究」中的部分受試者資料,使用者名稱與行為皆經過編碼處理。
線上操作平臺 / Online Workplace
以上的實作不需用到本機端的軟體,全部使用以下雲端服務。建議使用Google Chrome瀏覽器開啟:
計算器 / Calculator
行為序列資料格式 / Behavior sequential data format
儘管Bakeman跟Gottman在書中有介紹過幾種行為編碼的格式,但是我在考慮到從資料庫取得資料與記錄的方便性後,還是決定制訂一份比較簡單的行為序列資料格式。這個格式包含了三個欄位:
- 研究對象編號:可以是數字或文字,用來辨識不同的研究對象。
- 序列編號:必須是數字,用來表示行為順序。如果是時間格式,請把它換成數字,例如換成Unix時間。
- 事件:可以是數字或文字,用來研究對象在該時間點作的事情。如果研究對象在同一個時間點做了兩個事件,那可以用兩行相同的研究對象編號、序列編號,記錄不同的事件。
我在另一篇「循序樣式探勘:以Python的PrefixSpan實作」也是採用相同的格式。也就是說,同一份行為序列資料,我們既可以用滯後序列來分析,也可以用循序樣式探勘來分析。至於我早先寫的序列分析工具跟循序樣式探勘工具,就不要再使用了吧。
對滯後序列分析的誤解 / Misunderstanding about Lag Sequential Analysis
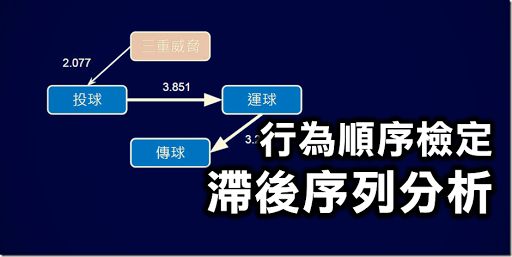
儘管這件事情我一直有在各個介紹中強調,但很遺憾的是,我還是常常聽到有人對序列分析結果有著錯誤的解讀方式。以上圖的表格來說,C->A的2次出現了顯著轉移,許多人就會解讀為「研究對象很常作C到A的動作」,但這樣解讀是錯誤的,這樣侯老師又要難過了。仔細看看表格的內容,不僅C->A是2次,連A->B與B->C也都是2次。顯然的,「很常作C到A的動作」這個說法並不合理,因為研究對象也很常作「A到B」與「B到C」啊。
那為何只有C->A的2次被視為顯著轉移呢?讓我們更仔細地閱讀表格,你會發現到研究對象只要作C的時候,下一個動作事件全部都會是A。另一方面,A之後的下一步可能會是A (1次)、B (2次)、C (1次);B之後的下一步可能會是B (1次)或C (2次)。可以看出C之後預測A的機率是100%,因此C->A才會顯著。詳細的公式就請參考投影片吧。
因此,我們不能說「研究對象很常作C到A的動作」,應該說「研究對象只要作了C,下一步很高的機會會做A」。至於研究對象到底很常作C->A、A->B、B->C的那種組合,不好意思,這不是滯後序列分析要回答的問題,但你可能可以在滯後序列分析找到這個答案,請見我所介紹的另一篇「循序樣式探勘:以Python的PrefixSpan實作」。
為什麼不用卡方檢定? / Limitation of Chi-square test
雖然滯後序列分析也是列聯表的一種分析方法,但是卻不是用卡方檢定來分析。這個原因在Bakeman與Gottman的書中也有說明。這是因為卡方檢定對資料有所要求,資料的樣本數量最好超過30以上,而列聯表的細格為0的數量不可以超過細格總數的1/4。但是在行為序列的事件轉移表中,研究對象不太可能會發生所有事件組合都平均做過數次的情況,因此勢必會有很多細格會以0表示。這就造成了行為序列轉換不能用卡方檢定,而是要用滯後序列分析的原因。
小結 / In closing
繼上一次卡方檢定講的太簡單,導致很快就教完的教訓。這次講滯後序列分析時我就特別花多點時間在介紹不同的例子、計算方式與滯後序列分析的延伸應用。這次調整授課方式的結果,反而讓整個授課流程稍微有點緊湊了,好像也應該適度地刪減一些內容啊?
不管怎麼說,在講過很多次滯後序列分析的研究後,我覺得這次教課的內容應該是最容易讓人理解,另外撰寫的滯後序列分析計算器也是至今為止最好用的一個。
而且這次的滯後序列分析計算器不僅只是算出報表,還有搭配結論寫作框架的文字結論,以及基於資料敘述級分析步驟所提到的「先把資料畫成圖」的原則,直接在網頁上呈現了行為序列轉移圖,我自己還蠻滿意的。
寫到這裡忽然想起來應該還要加上樣本敘述統計量的圓餅圖,不過這次就先這樣吧,如果下次還要講的話,我再來繼續改進。
這份滯後序列分析計算器做完後,就直接應用到該屆學弟妹的碩士論文中,分析出許多令人感興趣的結果,他們也就順利畢業了。而我,呃……還在寫blog……
紀念動物朋友 / For Kemono Friends
眼力不錯的讀者也許會發現本單元裡面出現了很多「動物朋友」的畫面。在教完這堂課的時候,有位學生很驚訝地跟我說:「原來老師也很宅!」但事實上這系列課程在第一堂介紹時就已經出現柯南跟Pokemon Go,第二堂資料的來源與形態時也有Pokemon跟死神等人物出場,看來要不是該同學的動漫知識不夠深,就可能是上課不夠認真吧?
事實上,我為了在本單元想一個合適介紹行為序列的例子,可真的是花了我許多時間。最後我才想比較容易理解的「遊客所在區域事件序列資料表」,這例子也剛好比較容易讓同學套用在其他的現實案例中。畢竟像Bakeman等人在書中舉的觀察研究法,是真正的行為研究者才會去做的事情啊。而這個例子也就很剛好地跟去年的熱門動畫動物朋友搭上線,所以我以此為教材來教序列分析。上課的時候的確蠻能吸引同學們的注意,甚至還有同學在教學評鑑的建議是:「老師講的動漫都是去年的,希望老師可以引用新一點的動漫」,這個我沒辦法,只好在精力旺盛的追番黨前給跪了。
(圖片來源:[達人專欄] 動物朋友撤換監督事件(燃燒的紙飛機))
話說回來,其實我在把授課內容投影片放到blog的時候,都會對內容做一些調整,以免帶來過於侵權的爭議。特別是動物朋友幾乎貫穿這整個單元,我本來是有在考慮換掉所有內容,改成其他插畫或照片。不過最近動物朋友發生了角川公司撤換關鍵人物監督たつき、引發眾多觀眾怒火的事件。一想到未來可能再也看不到動物朋友這樣兼具知識與樂趣、還能引發現象級熱潮的作品,我想還是繼續把動物朋友留在這個單元的投影片內吧。
關於動物朋友監督被撤換的事件的細節,請看等待著風的旅人所彙整的[達人專欄] 動物朋友撤換監督事件(燃燒的紙飛機)。
講到這邊,你對本單元的滯後序列分析有什麼看法呢?或是講到動物朋友,是否也讓你有些感慨呢?歡迎在下面留言說說你的想法,或是用左邊的AddThis按個讚或分享喔!














想請問如果想做的分析是,使用者進行了什麼網頁瀏覽的序列會導致銷售成功率上升,這也適用於行為序列分析嗎。如果是,感覺要把這一整串瀏覽的序列,最後再加上銷售成功/銷售失敗的事件。在分析序列產生後,只關心哪些序列會走到銷售成功 / 銷售成功,不知我這樣理解是否正確,又或這是另一種領域的分析了?
回覆刪除To angusivam,
刪除如果是要用序列分析的方法來看,那會變成「銷售成功組/銷售失敗組會進行什麼瀏覽序列*轉換*」
這樣子請先把網頁瀏覽序列分成兩組:銷售成功組 / 銷售失敗組
然後用片段(break)的方式組合各組裡面不同人的網頁瀏覽序列
https://docs.google.com/presentation/d/1uPTNQAXXSw9pxsy7-Q1RyHBb4XwB9JyTm_nBp38Cqcc/edit#slide=id.g167e18a6b9_0_238
最後可以比較不同組別的行為模式
https://docs.google.com/presentation/d/1SPyCUkx998B-fT2kYPSVwK7Lch_KwU7WoOdYTcYxdcY/edit#slide=id.g21b692f5b7_0_386
但比較不同組的時候,請不要用z分數比較,使用相關係數比較
https://docs.google.com/presentation/d/1SPyCUkx998B-fT2kYPSVwK7Lch_KwU7WoOdYTcYxdcY/edit#slide=id.g21b692f5b7_0_361
這樣就可以了
相關係數的計算方法請看投影片
但序列分析只能做到雙事件的分析,不能分析到三個以上的連續事件
https://docs.google.com/presentation/d/1SPyCUkx998B-fT2kYPSVwK7Lch_KwU7WoOdYTcYxdcY/edit#slide=id.g21ae494dc5_1_1506
要看行為順序預測的話,請用動態貝氏網路
http://blog.pulipuli.info/2017/10/behavior-prediction-dynamic-bayesian.html
謝謝您回覆的這麼詳細
刪除不客氣,我想您的問題應該也是很多人想知道的問題
刪除這樣整理一下應該對大家都有幫助喔
想請問您,用相關係數比較不同組,可以得出什麼樣的結論呢?
刪除假如實驗組C->A的相關係數大於對照組C->A的相關係數
我可以說「實驗組做C之後去做A的機會比對照組大」嗎?
To hui,
刪除不能說「實驗組做C之後去做A的機會比對照組大」
因為相關係數是跟其它事件轉移序列次數比較之後的結果
只能說「實驗組C->A事件轉移序列的相關程度高於控制組」
也就是對實驗組來說,相較於該組內的其它事件序列轉移,C->A的事件轉移序列相對頻率在排除掉樣本數量差異之後,其相關程度高於控制組。
不好意思,我想請問一下
回覆刪除因為有使用您的滯後序列分析計算器做計算
表格中有一列是用Yule's Q公式計算相關係數
我有去找Yule's Q相關文獻,但是看完該公式的定義,還是不懂如何將該公式套用並計算出結果
可以幫忙舉個例子或列出簡略計算過程嗎,感恩您
To Lin,
刪除關於Yule's Q公式計算相關係數的部分
在投影片108頁之後有講
https://docs.google.com/presentation/d/1SPyCUkx998B-fT2kYPSVwK7Lch_KwU7WoOdYTcYxdcY/edit#slide=id.g21b692f5b7_0_361
計算公式在投影片裡面。
不過回頭看看投影片,好像沒有講很多Yule's Q相關係數的事情。
簡單來說,Yule's Q相關係數會用於比較人數、序列長度不同兩組的序列上。
https://lh3.googleusercontent.com/-TOFEMXhdJVs/XA0hyTof2hI/AAAAAAAD7gE/mifXF4r8f18KO7Q4Dv905AxOPwWql7UTQCHMYCw/s0/2018-12-09_22-06-49.png
例如這張圖的「實驗組」跟「控制組」。
要比較兩組的時候,請不要用調整後殘差,應使用相關係數。
https://blog.pulipuli.info/2005/12/blogger_113544406852218769.html?showComment=1516262362587#c2290619181952601935
回覆刪除之前有位讀者提問,在按下計算器中「事件轉移表編輯器」下方的「增加事件編碼」按鈕之後,持續新增的編碼都會是G G G G。
我在某次修正後,按下增加事件編碼,編輯器會增加一個「E8」,再按下去會增加「E9」。這個是預設好的編號,意思是「Event No.8」、「Event No.9」。
但編輯器會強制依照字母順序排序,現在沒辦法自由調整喔。
老师,您好。
回覆刪除在您ppt60页中提到的错误结论,如果要描述1-》2-》的这样子的行为序列,还需要什么数据呢?您能具体阐释一下吗?
谢谢老师的回答
To yidanzhong,
刪除如果要解釋二階以上的事件序列,根據Roger Bakeman的建議,需要使用對數線性分析(log-linear analysis)。
對數線性分析是列聯表分析中三種以上類別屬性的分析方法。傳統的卡方獨立性檢定(the chi-squared test of independence)是檢測兩個類別變數間的關係,而對數線性模式則是用來分析更多類別變數時使用。
Bakeman所開發的程式ILOG下載位置如下:
https://bakeman.gsucreate.org/download-ilog/
但是光看軟體本身,仍然不能瞭解其意義。
關於對數線性分析應用於行為分析的用法,需要參考這本書:
Bakeman, Roger, and Byron F. Robinson. 2013. Understanding Log-Linear Analysis With Ilog: An Interactive Approach. Psychology Press.
但這本書我在臺灣找不到。
我也參考了其他介紹對數線性分析的書,有些書籍是寫「對數線性模型」、「三維列聯表分析」或是「三向列聯表分析」。但每本書的作法都不太一樣,而且大多是公式推演,找不到實際可用的工具,所以我就沒有特別繼續鑽研下去。
-------
因為從推論統計的角度似乎會越來越鑽牛角尖,所以我採取了另一種嘗試解決這個問題的方法:動態貝氏網路
這是用機器學習的方式,以貝氏網路演算法來建立預測模型。
關於動態貝氏網路的討論,請看這篇:
http://blog.pulipuli.info/2017/10/behavior-prediction-dynamic-bayesian.html
動態貝氏網路的建模很簡單,也很容易加入到系統應用中。
但是並不是用來檢定此模式是否達到非隨機性的作法。
-------
以前我做的序列分析可以看更長的觀察序列
http://blog.pulipuli.info/2010/12/sequential-analysis-tool.html
但這部分的公式是我自己提出來的,並非現有書籍或論文上的作法。
因此我不建議大家使用。
我對這個議題的瞭解大致上到這裡,歡迎討論。
作者已經移除這則留言。
回覆刪除最近發現了繪製社會網路圖的另一個好用的工具:sigma.js
回覆刪除http://sigmajs.org/
範例中的parallel-edges.html可以呈現出類似於滯後序列分析所需要的網路圖:
https://github.com/pulipulichen/sigma.js/blob/master/examples/parallel-edges.html
圖形展示:
https://pulipulichen.github.io/sigma.js/examples/parallel-edges.html
http://3.bp.blogspot.com/-aJ0w1HWMVEA/XPPCjTTMb-I/AAAAAAAEQw4/wL-Uu4DK_5oAiVfXA2c2K7VfU0FvGbi6ACK4BGAYYCw/s1600/2019-06-02_203310.png
這樣就能繪製事件轉移圖了。
原本我使用的jsPlumb缺乏力導向排版(force-directed layout)的演算法,所以只能自己手動拉節點來排版。
相較之下,sigma.js專業得多。
有機會再來把它實作出來吧。
匯出成SVG的語法請參考這個範例:
刪除https://github.com/pulipulichen/sigma.js/blob/master/examples/svg-export.html#L139
我最近需要分析有大量不同事件的資料,赫然發現這個JavaScript版本不能跑。
回覆刪除不能跑的原因是在瀏覽器上執行分析的速度過慢,又沒有使用非同步機制來緩衝,所以大量資料基本上是沒辦法分析的。
解決方法是使用PHP版本來分析:
http://blog.pulipuli.info/2016/10/php-introduction-of-behavior-coding-and.html
最近有朋友在問說為什麼工具不能運作。
回覆刪除這可能是我改到一半...然後就忘記改完它(遮臉)
你可以在這裡留言,提醒我記得把它修好。
也可以直接下載整個工具的程式碼,在你的電腦執行它。
所有的程式碼都擺在GitHub專案保存庫上:
https://github.com/pulipulichen/HTML-Lag-Sequential-Analysis
你可參考一下方法來下載整個程式碼:
http://blog.pulipuli.info/2016/05/github-how-to-download-files-in-github.html#postcatagithub-how-to-download-files-in-github.html0_anchor0
老師您好
回覆刪除我的資料是觀察受試者在完成任務的過程中出現的行為,每個受試者出現的行為次數差異相當大。我擔心滯後序列分析的方式將所有受試者資料合併計算,會產生偏誤(例如特定受試者有在行為A→B發生率異於其他人)。除了自己設定某些標準,例如總行為次數要低於多少,是否有其他解套辦法?也請老師推薦參考資料,謝謝。
您好,
刪除滯後序列分析的計算方式是綜合考量了比例和次數總數這兩種因素。根據您的敘述,您資料的差異是次數總數(行為次數差異相當大),但是您擔心的卻是比例差異(發生率異於常人)。
從上述可知,您是不是只是看到「滯後序列分析」就來用了,但並不知道「滯後序列分析」到底是在檢定什麼呢?
的確很多人直接將「行為分析」跟「滯後序列分析」畫上等號,不過您實作後就可以發現,其實並不是如此。
至於其他問題的回答如下:
# 1. 自己設定某些標準或是其他解套方法?
嗯,您要不要考慮其他直接檢定單次行為次數的統計方法,像是卡方獨立性檢定。
其實很多人想要分析的層次都只是單次行為的差異,並不是行為序列。
「為什麼您想要分析行為序列?」
除了有人跟您說行為分析就是滯後序列分析之外,如果您沒有什麼充分理由的話,那通常您的行為分析都只是在比較單次的行為次數而已。
關於卡方獨立性檢定的介紹,請看以下這篇:
https://blog.pulipuli.info/2017/10/correlations-with-categorical-variables.html
# 2. 行為次數要低於多少?
Bakeman的書中介紹了推薦最低的觀察樣本數量門檻。達到此門檻以上,顯著轉移才有實際上的意義。
有三種情況會影響門檻的高低:
1. 鄰近編碼可以相同的話,則需要更多樣本
2. 觀察編碼數量更多的話,則需要更多樣本
3. 欲觀察序列的序列越長的話,則需要更多樣本
相關的說明和計算公式請看這篇:
https://blog.pulipuli.info/2010/12/sequential-analysis-introduction.html
實務操作上,我幾乎看不到有人蒐集的資料量可以達到這個門檻。
主要原因是研究者想要分析的編碼數量過多,導致門檻拉得非常地高。
# 3. 請推薦資料
關於滯後序列分析,有基本概念的研究者,一律會推薦您看Bakeman的書。
Bakeman, R., & Gottman, J. M. (1997). Observing interaction: an introduction to sequential analysis. Cambridge: University Press.
作者已經移除這則留言。
回覆刪除作者已經移除這則留言。
回覆刪除最近有網友前來詢問關於滯後序列分析的問題。
回覆刪除1. 如何引用?
請引用Bakeman跟Gottman的原始書籍。
Bakeman, R., & Gottman, J. M. (1997). Observing interaction: an introduction to sequential analysis (2nd ed.). New York: Cambridge University Press.
檢定的算法請引用Allison跟Liker的論文
Allison, P. D., & Liker, J. K. (1982). Analyzing sequential categorical data on dyadic interaction: A comment on Gottman. Psychological Bulletin, 91(2), 393-403. doi:10.1037/0033-2909.91.2.393
真的很想要講的話再引用我的工具。
布丁布丁吃布丁(2017年3月10日)。行為順序檢定:滯後序列分析。布丁布丁吃什麼?。https://blog.pulipuli.info/2017/10/behavior-analysis-lag-sequential.html
2. 這個分析工具跟GSEQ的關係是?
沒有關係。
我是看書的內容來做的,製作的時候並不是參考GSEQ的做法。
有老師比較過GSEQ跟我的工具,發現結果不一樣。
實際上,滯後序列分析有很多不同的做法。
Bakeman跟Gottman的書中有很多論述。
總之目前這個工具是用Allison跟Liker的算法。
如果你想知道這個工具跟GSEQ的差別,可以自己去比較看看。
由於滯後序列分析的算法細節很多,我通常不能確定你的細節是什麼,也不確定GSEQ的原始碼是怎麼計算的,於是很難跟你說明它們之間的差異。
還是把問題回歸到原始的計算式吧。
如果想知道怎麼計算的話,這個滯後序列分析工具是開放原始碼,原始碼在GitHub。
https://github.com/pulipulichen/HTML-Lag-Sequential-Analysis
也許可能會有錯,歡迎自行驗證跟pull request修正。
3. 到底要看那個滯後序列分析工具?
目前是以現在這個網址的工具為主。
舊版的工具不再使用與維護。
https://blog.pulipuli.info/2017/10/behavior-analysis-lag-sequential.html
有網友在問僅分析有改變的序列的做法是怎麼做的。
刪除原始序列可能是:
「AABBCB」
如果設定僅分析有改變的序列,就是把重複的序列拿掉:
「ABCB」
就以調整後的結果來計算。
非常非常感謝你精彩且無私的分享~ 受益良多!!
回覆刪除To 見晴宮主,
刪除不客氣。
最近有朋友過來詢問輸入的資料分析時跟預期結果不符合的問題。
回覆刪除請注意輸入資料的格式必須遵循以下範例檔案:
https://docs.google.com/spreadsheets/d/1vJ96VhwRoH2OZ9vXzwFL2qsK46bEoLthA3akWGYkIbU/edit?gid=779108843#gid=779108843
第一列的資料「使用者編號 序列編號 事件」不會列入分析
望周知